|
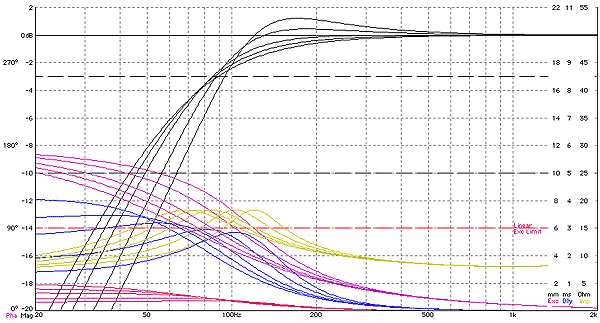
<clik chart
for larger chart>
The sealed box is most often executed
using sheet material which yields a rectangular box with the least amount of effort.
It is best to keep internal dimensions from being integral muliples of any other
dimensions. One of the best ways is to use ratios based on irrational numbers.
The table below uses one of the
world's favorite irrational numbers. This is the Golden Mean
-- 0.618... & 1.618... Feel free to use other irrational numbers (ie: epsilon,
square root of a prime number (don't use root 2 twice), pi). Of course you can use
any face to mount the driver -- as long as it is big enough.
|
Rectangular Box Internal Dimensions
(using Golden
Ratio 0.618:1:1.618)
|
|
VB (litres)
|
|
2.6
|
4.25
|
9.43
|
20
|
200
|
|
|
Height
|
|
8.8"
222 mm
|
10.3"
262 mm
|
13.5"
342 mm
|
17.3"
439 mm
|
37.3"
946 mm
|
|
Width
|
|
5.4"
138 mm
|
6.4"
162 mm
|
8.3"
211 mm
|
10.7"
271 mm
|
23.0"
585 mm
|
|
Depth
|
|
3.3"
85 mm
|
3.9"
100 mm
|
5.1"
131 mm
|
6.6"
168 mm
|
14.2
361 mm
|
|
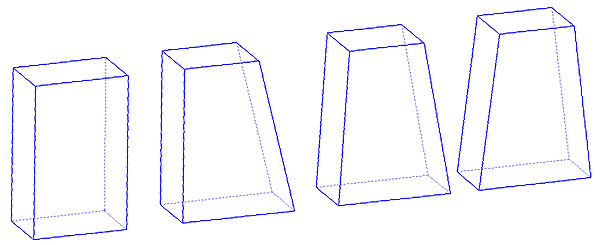
Boxes with walls that are non-parallel
tend to be better. Slanting the 2 largest panels is not that much harder and yields
what is termed a "pyramidal" box (even though not a true pyramid but a
trapezoidal cylinder). It is easy to change a rectangular set of dimensions to a
"pyramidal" box. If you subtract n units from the width of the top of the
box, add n units to the width of the bottom of the box. The shapes below give examples
based on the ratio used in the table.
You'll need to be a bit more creative
for even wilder shapes -- spheres, ellipoids, use of found objects like pots...
|